为什么大语言模型能懂“狮子”和“老虎”相似，却知道“狮子”和“桌子”差别很大？

你肯定会好奇，为什么大语言模型知道“狮子”和“老虎”是相似的，但是“狮子”和“桌子”区别很大。
这都归功于余弦相似性（Cosine Similarity）计算公式。

余弦相似度的历史发展

在1773年，Joseph-Louis Lagrange（约瑟夫-路易·拉格朗日）在研究三维四面体时，首次引入了点积和叉积的组件形式。

1843年，William Rowan Hamilton（威廉·罗文·哈密顿），通过四元数理论定义了向量运算，明确了点积的几何意义（|a| |b| cosθ），为余弦相似度的概念提供了理论框架。

1968年，被誉为“信息检索之父”Gerard Salton（杰拉德·索尔顿）在《Automatic Information Organization and Retrieval》中详细描述了向量空间模型，其中明确指定使用余弦相似度来计算向量的相似性。

在大语言模型中的实际应用

在大语言模型中，当字符被转换成词向量之后，余弦相似性公式是最常用的词向量相似性度量方法，它用于计算两个向量之间的夹角余弦值。

在公式中：

• 被除数是向量A和B的点积（dot product）。
• 除数是向量 a 的欧几里得范数（‖a‖）与向量 b 的欧几里得范数（‖b‖）的乘积。向量的欧几里得范数就像是向量的‘身高’，它用于归一化向量A和B的点积，确保结果只反映向量方向的相似性，而不受向量长度影响。

余弦相似性值范围在-1到1之间[-1, 1]

• cosθ = 1：如果结果值等于1，两个向量方向完全相同，表示两个向量最相似。两个完全一样的词向量（比如单词“cat”和“cat”）会有余弦相似度为 1。
• cosθ = 0：如果结果值等于0，两个向量垂直，表示无相似性。例如，单词“cat”和“table”可能接近垂直。
• cosθ ≈ -1：如果结果值等于-1，两个向量方向完全相反，表示最不相似（反向相关）。例如，单词“big”和“small”的词向量可能接近相反方向。

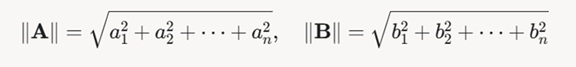
一个简单例子：计算“狮子”和“老虎”的词向量相似度

1. 现在我们假设“狮子”这个词被转换成词向量后等于1，2（ A=[1, 2]），而“老虎”这个词被转换成词向量后等于3，4（ B=[3, 4]）。
2. 按照公式, 第一步，我们先计算点积：
   向量 a 点乘向量 b 就是A⋅B=1 × 3 + 2 × 4 = 11。
3. 第二步，计算A，B两个向量的欧几里得范数
   依照公式我们知道，词向量A的欧几里得范数是：1的平方+2的平方再开根号，‖a‖ = √(1² + 2²) = √5 ≈ 2.236。结果约等于：2.236
   词向量B的欧几里得范数是：3的平方+4的平方再开根号，‖a‖ =√(3² + 4²) = 5.000000。结果等于：5
   把它们都代入公式：结果就约等于0.984

从这个结果可以看出，它非常接近于1。因此就说明两个词向量相似度非常高。

结语

怎么样？你学会了吗？